News

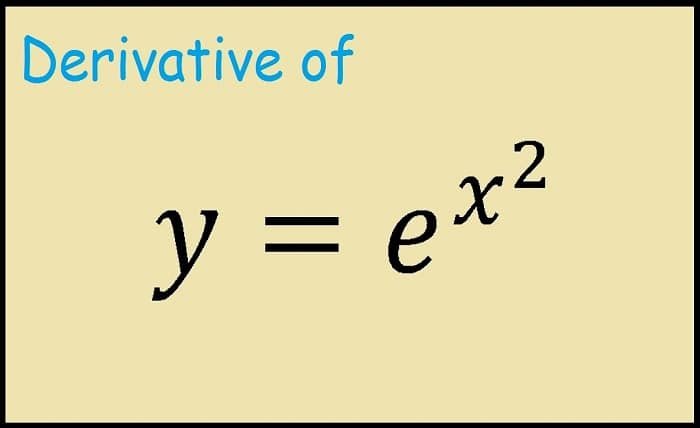
Derivative of e^4x: A Comprehensive Guide

JessyJune 27, 2024

0 0 3 minutes read

Introduction

The derivative of $e^{4x}$ is a fundamental concept in calculus that finds applications across various fields of science, engineering, and economics. Understanding how to differentiate exponential functions like $e^{4x}$ is crucial for solving complex problems and analyzing dynamic systems. In this blog post, we will delve deep into the derivative of $e^{4x}$ , exploring its calculation, significance, and practical uses.

Basics of Exponential Functions

Exponential functions are mathematical expressions where a constant base is raised to a variable exponent. The function $e^{4x}$ is a specific type of exponential function where the base $e$ (approximately 2.71828) is raised to the power of $4 x$ . This function grows rapidly and is essential in various natural and scientific phenomena.

Introduction to Derivatives

A derivative represents the rate at which a function changes concerning its variable. For $e^{4x}$ , the derivative helps us understand how the function’s value changes as $x$ varies. Differentiation is a core concept in calculus, providing insights into the behavior of functions.

Differentiation Rules

To find the derivative of $e^{4x}$ , we use specific differentiation rules. The chain rule is particularly useful here, allowing us to differentiate composite functions. For $e^{4x}$ , we recognize it as a composition of the exponential function and the linear function $4 x$ .

Applying the Chain Rule

The chain rule states that the derivative of a composite function is the derivative of the outer function evaluated at the inner function times the derivative of the inner function. For $e^{4x}$ , the outer function is $e^u$ (where $u = 4 x$ ), and the inner function is $4 x$ .

Step-by-Step Differentiation of $e^{4x}$

Let’s differentiate $e^{4x}$ step-by-step:

Identify the outer and inner functions: $e^u$ and $4 x$ , respectively.
Differentiate the outer function: The derivative of $e^u$ is $e^u$ .
Differentiate the inner function: The derivative of $4 x$ is 4.
Apply the chain rule: Multiply the derivatives: $e4x⋅4e^{4x} \cdot 4$ .
Simplify: The derivative of $e^{4x}$ is $4e^{4x}$ .

Significance of the Derivative $4e^{4x}$

The derivative $4e^{4x}$ indicates the rate of change of $e^{4x}$ with respect to $x$ . It shows how rapidly the function $e^{4x}$ increases as $x$ increases. This information is vital in understanding the growth patterns of exponential functions.

Graphical Representation

Graphing the function $e^{4x}$ and its derivative $4e^{4x}$ provides a visual understanding of their relationship. The graph of $e^{4x}$ is an exponential curve, and the graph of its derivative $4e^{4x}$ is a steeper exponential curve, reflecting the increased rate of change.

Real-Life Applications

The derivative of $e^{4x}$ finds applications in various real-life scenarios. In finance, it helps in modeling compound interest. In biology, it describes population growth. In physics, it is used in decay processes and wave functions. Understanding $4e^{4x}$ aids in solving these practical problems.

Common Mistakes to Avoid

When differentiating $e^{4x}$ , common mistakes include forgetting to apply the chain rule or incorrectly differentiating the inner function. Ensuring each step is followed accurately is crucial for obtaining the correct derivative $4e^{4x}$ .

Advanced Differentiation Techniques

Beyond the basic differentiation, advanced techniques can further simplify complex exponential functions. Techniques like logarithmic differentiation and implicit differentiation can be useful when dealing with more intricate functions involving $e^{4x}$ .

Integration of $e^{4x}$

Integration is the inverse process of differentiation. Knowing the derivative $4e^{4x}$ , we can find the integral of $e^{4x}$ . Integrating $e^{4x}$ involves recognizing the antiderivative, which is $14e4x+C\frac{1}{4}e^{4x} + C$ .

Practice Problems

Practicing differentiation of $e^{4x}$ reinforces understanding. Here are a few problems to try:

Differentiate $e^{4x + 2}$ .
Find the second derivative of $e^{4x}$ .
Differentiate $e^{4x^2}$ . These exercises help in mastering the differentiation of exponential functions.

Conclusion

The derivative of $e^{4x}$ is $4e^{4x}$ , a crucial concept in calculus with wide-ranging applications. Understanding the process of differentiating exponential functions enables us to solve complex problems in various fields. By mastering the differentiation of $e^{4x}$ , we gain deeper insights into the dynamic behavior of exponential growth and decay.

FAQs

1. What is the derivative of $e^{4x}$ ?

The derivative of $e^{4x}$ is $4e^{4x}$ .

2. Why is the chain rule important for differentiating $e^{4x}$ ?

The chain rule is important because it allows us to differentiate composite functions, such as $e^{4x}$ , by breaking them down into simpler parts.

3. Can the derivative of $e^{4x}$ be used in real-life applications?

Yes, the derivative $4e^{4x}$ is used in various fields, including finance, biology, and physics, to model growth, decay, and other dynamic processes.

4. What is a common mistake when differentiating $e^{4x}$ ?

A common mistake is forgetting to apply the chain rule or incorrectly differentiating the inner function $4 x$ .

5. How do you integrate $e^{4x}$ ?

To integrate $e^{4x}$ , recognize the antiderivative: $dx=14e4x+C\int e^{4x} \, dx = \frac{1}{4}e^{4x} + C$ .