When dealing with mathematics, particularly factors and multiples, it’s essential to understand the basics. The factors of 42, specifically when paired, form the foundational elements for various mathematical applications and problem-solving scenarios. This post delves into the factors of 42, exploring each pair in detail.
What Are Factors?
Factors are numbers that divide another number without leaving a remainder. Discussing the factors of 42 means looking at all numbers that can divide 42 perfectly. This concept is fundamental in various branches of mathematics, including algebra and number theory.
Why Focus on the Factors of 42?
The number 42 is significant in mathematics due to its properties and the ease with which it can be used to teach basic factorization techniques. Understanding the factors of 42 in pairs is particularly useful for students and educators alike.
How to Determine Factors
Determining the factors of a number involves division. To find the factors of 42, one would test each integer to see if it divides 42 without leaving a remainder. This section will explain the process step-by-step.
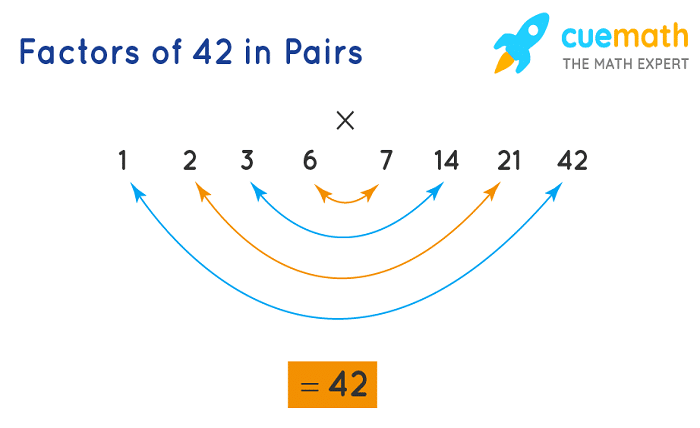
Pairing Factors of 42
Every factor has a corresponding pair that multiplies together to give 42. This section lists and explains each pair, enhancing understanding of how multiplication and division are intertwined.
The Significance of Each Pair
Each pair of factors has its own significance, often used to solve specific mathematical problems. This part of the post explores the importance of each factor pair of 42 in mathematical equations and real-world applications.
Visualizing Factor Pairs
A visual aid, such as a factor tree or a simple diagram, can help visualize the factor pairs of 42. This can be particularly helpful for visual learners.
Factors of 42 in Education
In educational settings, the factors of 42 can be used as a practical example to teach basic arithmetic operations and introduce algebraic concepts. This section discusses how teachers can effectively use these factor pairs in the classroom.
Factors and Their Role in Problem Solving
Understanding factors, including those of 42, is crucial in solving higher-level mathematical problems. This includes problems in algebra, geometry, and beyond.
Advanced Applications of Factors
Beyond basic education, the factors of 42 play roles in more advanced areas, including number theory and computer science. This section delves into some of these sophisticated applications.
Common Misconceptions About Factors
Many students and even some educators have misconceptions about factors. This part of the post aims to clarify these misunderstandings, specifically regarding the factors of 42.
Factors of 42 in Everyday Life
Though seemingly a pure mathematical concept, the factors of 42 find their applications in everyday life, including in scheduling problems, technology, and even in popular culture.
Tips for Remembering Factor Pairs
This practical section offers tips and tricks to easily remember the factors of 42 and their pairs, useful for both students and teachers.
Conclusion
The factors of 42, especially when examined in pairs, offer a fascinating glimpse into the world of numbers. Whether for educational purposes or advanced mathematical applications, understanding these factor pairs is beneficial. Embracing this knowledge can open doors to a deeper understanding of mathematics and its practical applications in real life.
FAQs
1.What are the exact factor pairs of 42?
The factor pairs of 42 are (1, 42), (2, 21), (3, 14), and (6, 7).
2.Why is it important to learn about factors?
Learning about factors helps in simplifying many mathematical operations and is fundamental in developing problem-solving skills.
3.Can the factors of 42 be used in real-world applications?
Yes, understanding factors can be applied in areas like time management, architecture, and technology design.
4.Are there any tricks to quickly find the factors of any number, not just 42?
A good trick is to start with the smallest and largest numbers (1 and the number itself) and work inward, checking divisibility.
5.How can educators make learning about factors more engaging?
Educators can use games, puzzles, and interactive technology to make the learning process about factors, including those of 42, more engaging and interactive.





