Factor Pairs of 125: A Comprehensive Guide
Introduction
Factor pairs of a number are two numbers that, when multiplied together, give the original number. For the number 125, understanding its factor pairs is straightforward but interesting due to its properties as a composite number primarily composed of a single prime factor repeated.
What Are Factor Pairs?
Before delving deeper into the factor pairs of 125 specifically, it’s crucial to grasp what factor pairs are in general. This section will provide a foundational understanding of factor pairs, setting the stage for more specific discussions.
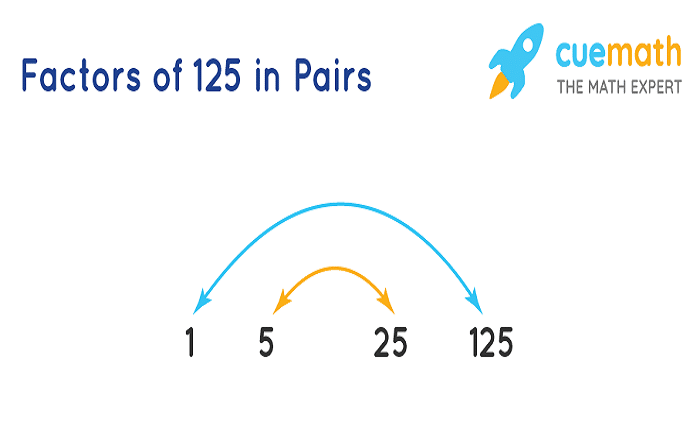
Factor Pairs of 125 Explained
Here, we explore the specific factor pairs of 125. This number, being a perfect cube, offers a unique set of factor pairs which we will list and explain in detail, ensuring clarity on how these pairs are derived.
The Significance of Prime Factors in 125
125 is particularly interesting due to its composition of prime factors. This section will discuss the role of the number 5, the sole prime factor of 125, and how it contributes to determining the factor pairs of 125.
Mathematical Applications of Factor Pairs
Understanding the factor pairs of 125 opens up various mathematical possibilities. This part of the blog will explore different scenarios where knowing the factor pairs of 125 can be practically applied, from simplifying square roots to solving real-world problems.
Factor Pairs and Their Role in Problem Solving
Here, we’ll see how the factor pairs of 125 can be used to simplify complex mathematical problems, providing practical examples that demonstrate their utility in problem-solving scenarios.
Teaching Factor Pairs in Education
For educators, explaining the concept of factor pairs, particularly for a number like 125, can enhance students’ understanding of basic multiplication and division concepts. This section provides tips and strategies for teaching factor pairs effectively.
Factor Pairs in Number Theory
This section delves into the deeper mathematical implications of the factor pairs of 125 within the field of number theory, discussing how they relate to concepts like divisors and multiples.
Advanced Concepts Linked to Factor Pairs of 125
Beyond basic arithmetic, the factor pairs of 125 have implications in more advanced areas of mathematics, including algebra and geometry. This segment explores these advanced concepts and how they relate back to the factor pairs of 125.
FAQs on Factor Pairs of 125
Addressing frequently asked questions, this part of the blog post aims to clarify any common misconceptions and provide further insights into the factor pairs of 125, enhancing reader understanding through a Q&A format.
Conclusion
The factor pairs of 125 provide more than just numbers to multiply; they offer insights into the structure of numbers and their properties. Whether for educational purposes or as part of deeper mathematical exploration, understanding these factor pairs can enrich one’s knowledge and appreciation of math.
FAQs
1. What are the factor pairs of 125?
The factor pairs of 125 are (1, 125) and (5, 25). These pairs multiply to give the product of 125.
2. Why are there only two factor pairs for 125?
125 is a cube of the prime number 5 (5x5x5). Its unique prime factorization contributes to having a limited number of factor pairs.
3. How can knowing the factor pairs of 125 help in solving problems?
Knowing the factor pairs of 125 can simplify multiplication and division processes, aid in factorization problems, and help in finding the least common multiple and greatest common divisor in more complex arithmetic operations.
4. Can the factor pairs of 125 be used in real-world applications?
Yes, understanding factor pairs can help in various real-world contexts, such as financial calculations, computing dimensions, and optimizing resources.
5. What is the educational significance of teaching factor pairs?
Teaching factor pairs helps students understand the concepts of multiplication and division more deeply, enhances their problem-solving skills, and lays a strong foundation for more advanced mathematical concepts.