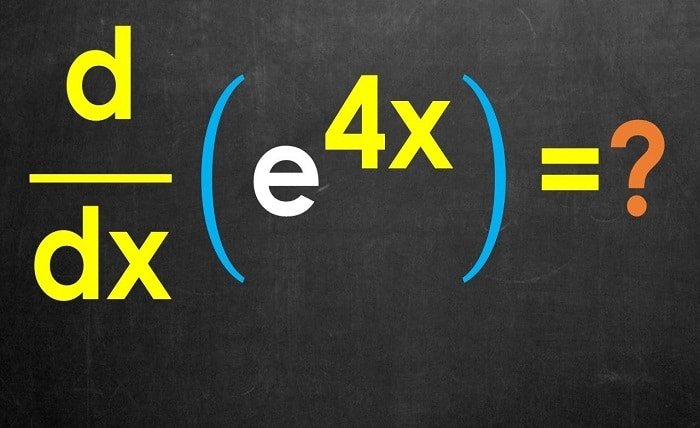
Introduction
When dealing with exponential functions, finding derivatives can be a crucial skill, especially in calculus. One common function that often appears in mathematical problems is e^4x. Understanding how to derive this function is not only fundamental for solving complex equations but also for grasping the broader concepts of exponential growth and decay. In this blog post, we will explore the derivative of e^4x in detail, covering the basics, rules, and applications.
What is e^4x?
The function e^4x is an exponential function where the base is the natural number e (approximately 2.71828), and the exponent is a linear term 4x. Exponential functions like e^4x are essential in many fields, including mathematics, physics, and engineering, due to their unique properties and the role they play in modeling exponential growth and decay.
Basic Rules of Differentiation
Before diving into the derivative of e^4x, it’s essential to understand some basic rules of differentiation. These rules include the power rule, the product rule, the quotient rule, and the chain rule. Each of these plays a vital role in differentiating various types of functions, including exponential functions like e^4x.
The Chain Rule
The chain rule is particularly important when differentiating composite functions. For the derivative of e^4x, the chain rule states that if a function y can be expressed as a composite of two functions u and v, then its derivative is the derivative of the outer function evaluated at the inner function times the derivative of the inner function. This rule is crucial for finding the derivative of e^4x.
Differentiating e^x
To understand the derivative of e^4x, it helps to start with a simpler exponential function, e^x. The derivative of e^x with respect to x is e^x. This property is unique to the exponential function with base e and serves as a foundation for differentiating more complex exponential functions like e^4x.
Applying the Chain Rule to e^4x
Now, let’s apply the chain rule to find the derivative of e^4x. First, identify the outer function (e^u) and the inner function (4x). According to the chain rule, the derivative of e^u is e^u times the derivative of u. For e^4x, u is 4x, and the derivative of 4x with respect to x is 4. Therefore, the derivative of e^4x is e^4x times 4.
Step-by-Step Derivation
Here’s a step-by-step process to find the derivative of e^4x:
- Identify the outer function (e^u) and the inner function (4x).
- Differentiate the outer function with respect to the inner function: d(e^u)/du = e^u.
- Differentiate the inner function with respect to x: d(4x)/dx = 4.
- Apply the chain rule: (d/dx)e^4x = e^4x * 4.
Thus, the derivative of e^4x is 4e^4x.
Verification of the Result
To ensure the correctness of our derivative of e^4x, we can verify by plugging in values and using numerical methods or software tools to check the result. This verification process helps solidify the understanding and accuracy of our differentiation.
Graphical Interpretation
Graphically, the function e^4x represents exponential growth. The slope of the tangent to the curve at any point gives the rate of change of the function, which is the derivative. For e^4x, this rate of change is 4e^4x, indicating how steeply the function increases as x increases.
Applications in Real Life
The derivative of e^4x appears in various real-life applications, including population growth models, radioactive decay, and financial calculations involving compound interest. Understanding how to derive and interpret this function can provide valuable insights into these fields.
Common Mistakes to Avoid
When finding the derivative of e^4x, common mistakes include forgetting to apply the chain rule or miscalculating the derivative of the inner function. Double-checking each step and practicing with different exponential functions can help avoid these errors.
Advanced Topics: Higher-Order Derivatives
For those interested in more advanced topics, exploring higher-order derivatives of e^4x can be enlightening. The second derivative, for instance, involves differentiating the first derivative again, resulting in 16e^4x. Higher-order derivatives continue to follow this pattern, providing deeper insights into the function’s behavior.
Practice Problems
To master the derivative of e^4x, practice is essential. Here are a few practice problems to try:
- Differentiate e^4x + 3x^2.
- Find the second derivative of e^4x.
- Solve for the derivative of e^(4x + 2).
These problems will help reinforce the concepts and techniques discussed in this post.
Conclusion
The derivative of e^4x is a fundamental skill in calculus, essential for solving a wide range of mathematical problems. By applying the chain rule and following a step-by-step process, you can confidently find the derivative and apply it in various contexts. Whether you’re a student, a teacher, or a professional, mastering this derivative enhances your mathematical toolkit and opens up new possibilities for analysis and application.
FAQs
1. What is the derivative of e^4x?
The derivative of e^4x is 4e^4x. This is found using the chain rule, where the outer function is e^u and the inner function is 4x.
2. Why is the chain rule important for finding the derivative of e^4x?
The chain rule is essential because it allows us to differentiate composite functions. For e^4x, it helps us account for the inner function 4x while differentiating the outer exponential function.
3. Can you provide an example of a real-life application of the derivative of e^4x?
One real-life application is in modeling population growth. If a population grows exponentially at a rate proportional to e^4x, the derivative 4e^4x represents the rate of population increase at any given time.
4. What are common mistakes to avoid when differentiating e^4x?
Common mistakes include not applying the chain rule correctly or miscalculating the derivative of the inner function. Ensuring each step is accurate helps avoid these errors.
5. How can I practice finding the derivative of e^4x?
Practicing with a variety of exponential functions and composite functions can help. Try differentiating functions like e^(4x + 5) or combining e^4x with polynomial terms to solidify your understanding.





